What is a Mirror?
A mirror is made of glass that is coated with a metal amalgam on one side due to which the light ray incident on the surface undergoes reflection and not refraction.
Similar to lenses, even mirrors can form images that have a variety of properties. For instance, makeup mirrors form an enlarged version of the object in front it. While, car side view mirrors and shop security mirrors form a miniature version of the objects in front.
It follows the law of reflection which is – the angle of incidence is equal to the angle of reflection.
Sign Convention for Spherical Mirror
While doing calculation related to mirrors, like the calculation to find out magnification or using the mirror formula, there a set of rules that need to be followed while deciding if the value is positive or negative.
Sign convention is a set of rules that standardises a set of signs for the distances that are calculated in ray diagrams for the purpose of mathematical analysis of image formation.
Distances and the signs are always taken from the pole of the spherical mirror.
- The distance measured along the direction of the incident ray (measured from behind the spherical mirror surface) is always taken as a positive value
- The distance measured opposite to the direction of the incident ray (that is towards the object along the principal axis) is always taken as a negative value.
- The height that is measured above the principal axis is taken as positive
- The height measured below the principal axis is taken as a negative value.
Even if sign convention is reversed, it will give us the same results.
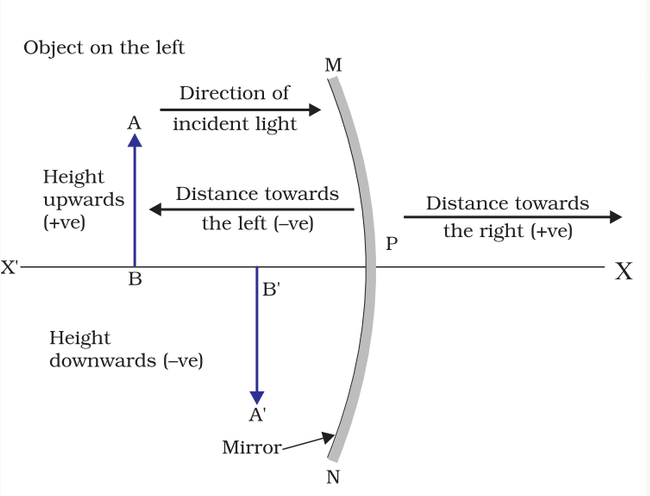
Sign convention in the case of a concave mirror
First let us briefly revise what a concave mirror is. Concave mirrors are a type of spherical mirrors that have curved surfaces and are painted on the outer side. This becomes an inner surface reflecting mechanism. Light converges at a point when it first strikes the surface and then is reflected back.
- The object is always placed in front of the mirror so the object distance is always taken as negative distance.
- The centre of curvature and the principal focus of the concave mirror lie in front of the mirror (on the same side as the object) so in this case the focal length along with the radius of the curvature is taken as negative distances.
- In case of concave mirrors, the image formed can be in front of or behind the mirror. When the image formed is in front of the mirror, the image distance is a negative value. But when the image formed is behind the mirror, the image distance is taken a positive.
- The nature of the image decides whether the height of the image will be taken as positive or negative. If the image is upright, that means above the principal axis, the height of image is positive. But if it is inverted and lies below the principal axis, the image height is a negative value.
Sign convention for a convex mirror
Again, let us first briefly revise what a convex mirror is. Convex mirrors are spherical mirrors that have curved surfaces but unlike concave, the inner side is painted and not the outside. So, this has an outer surface reflecting mechanism. This type of mirror diverges light when it strikes the reflecting surface. The images formed are always virtual, erect and diminished.
- The object is always placed in front of the mirror so the object distance is always taken as negative distance.
- The center of curvature and the principal focus of the convex mirror lie behind the mirror (on the opposite side of the object) so in this case the focal length along with the radius of the curvature is taken as positive distances.
- Convex mirrors always form an image behind the convex mirror. This means the distance of the image is taken as positive a it is along the direction of the incident ray.
- The nature of the image decides whether the height of the image will be taken as positive or negative. But in the case of convex mirrors, the image formed is always a virtual image (that is upright in nature and lies above the principal axis). This is why the height of the image is a positive value.
Mirror Formula
Where f is the focal length
v: the distance that lies between the image and the optical centre of the lens
u: the distance that lies between the object and the optical center of the lens
Magnification
When an object is placed in front of the mirror, the image formed might appear to differ in size compared to the object. The image is then called to be magnified. To find the value by which the image is magnified, we use a formula that is derived by the definition of lateral magnification.
where m = magnification, hi = height of the image and ho = height of the object
This is a dimensionless (unit less) quantity as the numerator and denominator have the same dimension which cancel out each other.
The quantity lateral magnification can also be calculated using its relation with the image distance and object distance. The equation is as follows
where m = magnification, ox’ = the image distance, ox = the object distance
If the value of lateral magnification is one, the size of the image and object are the same. If the value of lateral magnification is greater than one, the image is enlarged. And if lateral magnification is less than one, the image is diminished.
If there is a positive magnification, the image formed is a virtual image (the image formed is erect) but if the magnification is negative the image formed is a real image (the image formed is inverted).
Context and Application
This topic is studied in
- Bachelors in Science (Physics)
- Master In Science (Physics)
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.